• Optimization
• gradient Method(梯度法)
  • 搜索方向
  • 归一化(feature scaling?)
  • Gradient Descent(梯度下降法)
    • principle(原则)
    • batch gradient Descent(full gradient descent)
    • mini-batch gradient descent
    • stochastic gradient descent
  • Newton(牛顿法)
    • BFGS(变尺度法)
    • L-BFGS
  • conjugate gradient
• references(参考)

Overview
在给定的loss function情况下，采用一种算法帮我们找到该loss function的最小值或者接近最小值。
即：minimize loss(X,y,\(\Theta\))。
机器学习的问题最终都会归结为对一个优化问题进行求解，而优化问题可以分为无约束优化问题和有约束优化问题。有约束的优化问题是指对于目标函数中的变量有显式约束条件的，比如0<=x<=100。
无约束优化问题是指对于目标函数的变量没有显式约束的，或者说可以将约束转化成目标函数的惩罚项的，比如说正则化项。
大多数机器学习问题最终都要解一个无约束的优化问题，因此本文主要对无约束优化问题及其优化算法做一个概述。下文提到的优化问题都指无约束优化问题。

Optimization

在函数满足一些限制的情况下，找到一个工具或者办法使得该函数最小。
$\underset{x}{minimize} f(x)$
s.t. $g(x) = 0; x > 0;$

eg.

• linear regression:
  $\underset{\Theta}{minimize} ||\Theta X - y||^2$
  
• classification(logistic regression or SVM)
  $\underset{\Theta}{minimize} \sum_{i=1}^{i=m} log(1 + e^{-y_i X_i^T \Theta})$

gradient Method(梯度法)

两个关键点：搜索方向和归一化(feature scaling?)

搜索方向

在直线搜索的方式中，算法首先选择一个搜索方向（不同的算法选择的搜索方向不同）\(p_k\)，然后沿着这个方向从\(x_k\)开始去搜索\(x_{k + 1}\)，使得目标函数在(x_{k+1}\)处的值要更优于在\(x_k\)处的值。现在的问题是要沿着\(p_k\)走多长，才能找到最优的\(x_{k+1}\)，所以在直线搜索中，一旦搜索方向确定了之后，搜索的是这个步长t的值。这可以通过下面的公式获得： $min_{t>0} f(x_k + \mu *p_k)$
通过求解上式，我们可以得到最优的\(\mu\)值，但是在实践中，这样做的代价是十分大的，也没有必要，因此实践中只需要找到一个最小值的近似就可以了，也就是说\(f(x_{k+1})\)的值相对于\(f(x_k)\的值有足够的减小即可。在得到\(x_{k+1}\后，算法会重新计算新的迭代方向和步长。如此往复，直到最终问题求解。
对于直线搜索，我们已经提到了不同的算法会选择不同的搜索方向。这里我们介绍两个方向，一个是最速下降方向（steepest descent direction），另一个是牛顿方向（newtown direction）。前者对应的是目标函数的一阶导数，而后者对应的是目标函数的二阶导数。

归一化(feature scaling?)

有时候优化算法的性能取决于问题的形式。这其中一个重要的方面就是模型参数（目标函数系数）的归一化。当目标函数的某一个变量发生变化时，它使得目标函数的值发生很大的变化，而在另外的变量上做相同的改变时，目标函数值的变化远远不及上述变化，那么这个问题被认为是没有归一化的。
在机器学习 - feature scaling中会进行详细的讲解。

Gradient Descent(梯度下降法)

Gradient Descent几乎是全世界目前为止最简单有效的优化算法。
算法如下：
Repeat to minimize \(f_{\Theta}(X, Y, \Theta)\) :
$\theta_i = \theta_i - \mu \frac{\partial f_{\Theta}(X, Y, \Theta)}{\partial \theta_i}, i = 1,2,\cdots,n$
其中 \(\Theta = \begin{pmatrix} \theta_0, \theta_1, \theta_2, \cdots, \theta_n \end{pmatrix} \), \(\mu\)为learning rate.
该算法所选择的搜索方向为最速下降方向，其中\(p_k = \frac{\partial f_{\Theta}(X, Y, \Theta)}{\partial \theta_k}\)。

principle(原则)

• learning rate的选择
  选择一个足够小的值，确保loss function的值不会发散，最后收敛于一个稳定额值。如下图所示：
  

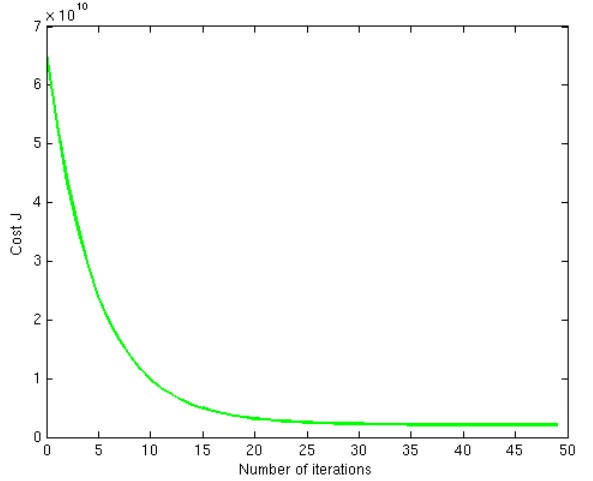
batch gradient Descent(full gradient descent)

计算损失函数在整个训练集上的梯度方向，沿着该方向搜寻下一个迭代点。”batch“的含义是训练集中所有样本参与每一轮迭代。
损失函数如下：
$Loss(X,Y,\Theta) = \frac{1}{2m} * \sum_{i=1}^{m}(h_{\theta}(x^i) - y^i )^2$
训练算法如下：
repeat \(minimize Loss\):{
$\theta_j = \theta_j - \frac{\alpha}{m} * \sum_{i=1}^{m}(h_{\theta}(x^i) - y^i ) * x_j^i$
}

mini-batch gradient descent

假设训练集有m个样本，每个mini-batch（训练集的一个子集）有b个样本，那么，整个训练集可以分成m/b个mini-batch。我们用ω表示一个mini-batch, 用Ωj表示第j轮迭代中所有mini-batch集合，有： $\Omega = \{w_k:k=1,2,\cdots,\frac{m}{b}\}$
算法如下：
repeat {
repeat {
$\theta_j = \theta_j - \frac{\alpha}{b} * \sum_{i=1}^{b}(h_{\theta}(x^i) - y^i ) * x_j^i$
} for (k = 1,2,…,m/b)
}

stochastic gradient descent

随机梯度下降算法（SGD）是mini-batch GD的一个特殊应用。SGD等价于b=1的mini-batch GD。即，每个mini-batch中只有一个训练样本。
应用：主要用于online learning

Newton(牛顿法)

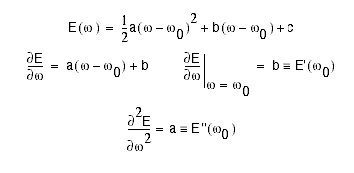
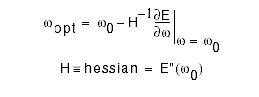
如上图所示，牛顿算法使用数学的方式，一步达到最优的参数值。

缺点：在进行海量数据计算时，计算H(hessian)的逆需要大量的空间和时间，成本太高。

BFGS(变尺度法)

属于quasi-Newton方法中的一种

L-BFGS

在生产环境中，使用最多的一种。

conjugate gradient

references(参考)

1. 机器学习的优化算法概述
2. Optimal Weight and Learning Rates for Linear Networks
3. book:”Introduction to Convex Optimization for Machine Learning” by John Duchi
4. Approximations Of Roots Of Functions – Newton’s Method
5. batch-GD， SGD， Mini-batch-GD， Stochastic GD， Online-GD – 大数据背景下的梯度训练算法