Overview(概述):
Linear Regression(线性回归)属于supervised Learning(监督学习),因此方法和监督学习的应该是一样的。
即:根据样本集的训练数据,学习得到一个线性函数的参数。最后使用该参数的线性函数来预测为训练的数据。
Definition(定义)
Linear Function:
一个样本 (x,y), \(
x = \begin{pmatrix}
x_1, x_2, \cdots , & x_n
\end{pmatrix}
\)
,具有\(x_1,\cdots,x_n\) feature(特性),其中y是一个具体的数值,参数为:
\(
\Theta = (\theta_0,\theta_1,\theta_2,\cdots,\theta_n)
\)
线性函数的公式如下:
上述公式展开之后如下:
loss function(成本函数)
(X_i,yi)表示第i个样本,用
\(
X = \begin{pmatrix}
X_1^T, X_2^T, \cdots, X_m^T
\end{pmatrix}
\)表示所有的样本输入集合, \(
Y = \begin{pmatrix}
y_1,y_2,
\cdots,
y_m
\end{pmatrix}
\) 表示所有的样本输出集合。
Target(目标)
找到一个\(\Theta\),从而使得loss function最小。
最终生成的线性模型如下:
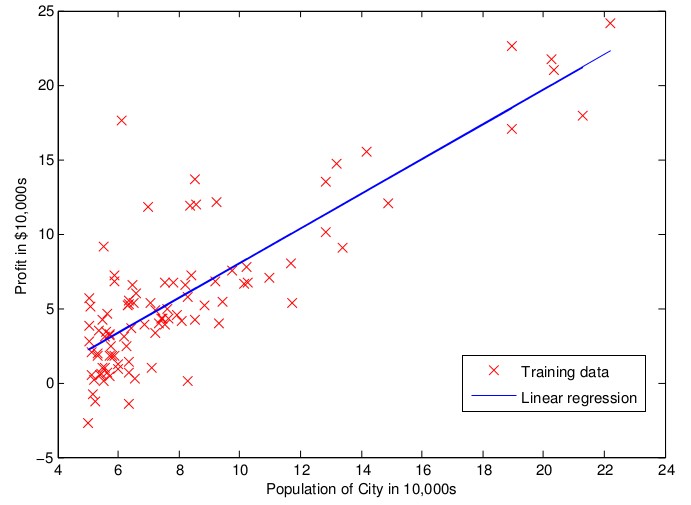
solutions(方案)
gradient Descent (梯度下降)
Repeat to minimize Loss(X,\(\Theta,Y\)) :
{
}
注意:此时的gradient Descent为Batch Gradient Descent(BGD)
前置条件 先对输入的各个特征进行feature scaling,具体请从参考feature normalization。
principle(原理)
对loss function进行\(\Theta\)中各个parameter:\(\theta_i\)(参数)进行求导,得到的导数\(\frac{\partial loss(X,y,\Theta)}{\partial \theta_i}\)即为该参数的倾斜度。
迭代下面的运算得到新的\(\Theta\),代入到loss function中得到新的值,直到这个变得稳定为止(即 \(\frac{\partial loss(X,y,\Theta)}{\partial \theta_i}\approx 0\))。
如下图所示,说明我们选择了一个恰当的learning rate:\(\mu\),我们可以选择\(iteration=30\)处所得到的\(\Theta\)作为我们最终模型的参数:
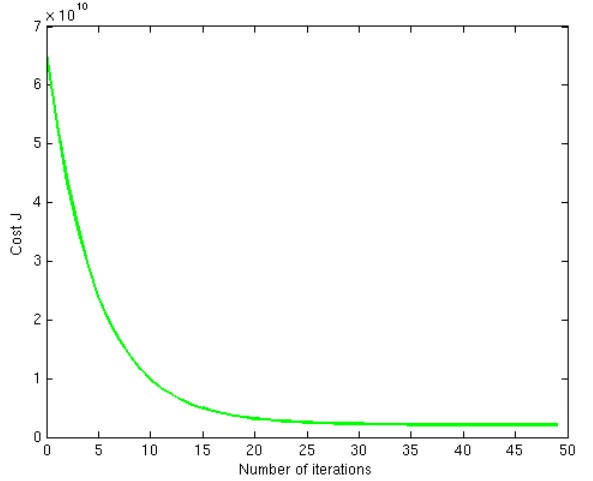
问题
如果没有经过feature normalization,很有可能会出现各个参数\(\theta_i\) 的learning rate:\(\mu\) 不一样的情况,
我们就无法得到一个适用于所有参数的global learning rate。
有时候会出现局部最小值,或者平原情况,这个时候为了求取最小成本函数,我们迭代的次数就会增多,有时会停留在local mininum。
而BGD无法解决这个问题。
normal equations(正规方程)
对成本函数的变量:\(Theta\)求导如下,如果得到的值为0,则表示成本函数达到了最底部,我们找到了最有的\(\Theta\)。
得到:
当维度很高的时候,计算矩阵的逆代价会很昂贵。
Regularization(正规化)
cause(起因)
有时候虽然我们达到了将loss function的值降到最小,但是该模型却不能很好地对新来的样本进行成功的预测, 或者不如比loss function的值小的模型预测的准确。就是因为该模型已经过度拟合(under-fitting and over-fitting)了
solution(解决方案)